mousetrap vehicle science

Mousetrap Vehicles: Rotational Inertia

Rotational inertia is the resistance an object has to changes in it's state of rotation. For an object that is not rotating we commonly talk about its inertia or its mass; the more mass an object has, the more resistance the object will have to any change in it's state of motion. With rotational inertia we still talk about an objects mass but we also include the location of it's mass with respect to it's point of rotation. The greater the distance between the average mass of a rotating object and it's point of rotation means the greater the rotational inertia of the object. Torques are required to change an objects state of rotation. The more rotational inertia an object has the more torque that will be required to change the objects state of rotation.

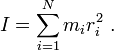
formula: rotational inertia [I] depends on the average location of the mass [m] times the radius [r] squared. Rotational inertia is measured in kilograms times meters squared, mass is measured in kilograms, and the radius is measured in meters.

rotational inertia: different wheels have different amounts of inertia depending on their size and the location of their mass from center.

Rotational Inertia and Wheels

Wheels are an important part of any vehicle and have a huge impact on the overall performance. If you are building a super-fast speed-trap racer then rotational inertial is one of the most important concepts you will need to understand. The secret to winning any top-speed mouse trap contest is to get your vehicle to the finish line in less time than everyone else; what this really means is that you will need to out acceleration the rest of the competition. In all top-speed contest inertia is the biggest problem a mousetrap vehicle will have to over come in order to be successful; and for this reason, wheels must be carefully selected to have as little rotational inertia as possible. Remember that wheels require a torque to change their stated of rotation and the more rotational inertia a wheel has the more torque that will required to changes it's state of rotation. In an acceleration race between two wheels, one a hoop and the other a disk, both with the same mass and the same size the disk will win because its average mass is located closer to the wheels center; BUT, if mass can be removed from the hoop it can have even less rotational inertia than the same disk.

I = (1/2) × mr²

inertia of a disk: the rotational inertia of a disk it defined as one-half the total mass [m] times the radius [r] squared. Rotational inertia is measured in kilograms times meters squared, mass is measured in kilograms, and the radius is measured in meters.

I = mr²

inertia of a hoop: the rotational inertia of a hoop it defined as the total mass [m] times the radius [r] squared. Rotational inertia is measured in kilograms times meters squared, mass is measured in kilograms, and the radius is measured in meters.

Rotational Inertia and Torque

Torques are required to change the state of rotation for any rotating object. A toque is the perpendicular component of a force that is applied some distance from the point of rotation.. The greater the torque applied to a rotating object the greater the change in its state of rotation. When you open a door you applied a torque, you either pull or push on the door and this causes it to rotate and open. Imagine if instead of pushing or pulling on the outside of the door you repositioned the handled closer to the hinge, because the radius is now smaller it will take a lot more force to open the door than compared to the normal situation.

τ = Fr

torque: a torque [τ] is equal to a force [F] applied a distance [r] from it's rotating center. Torque is measured in newton meters, force is measured in meters, and the radius is measured in meters.

τ = Iα

torque: a torque [τ] is also defined as the rotational inertia [I] of an object times the angular acceleration [α]. Torque is measured in newton meters, rotational inertia is measured in kilograms times meters squared, angular acceleration is measured in radians per second squared.

Rotational Inertia and Energy

The true kinetic energy of a wheel is a combination of its linear speed and it's rotational speed. All rotating objects have kinetic energy that depends on and objects rotational inertia and the rate at which the object is rotating.

KE_rotational = (1/2) × Iω²

rotational energy: the kinetic energy [ke] of a rotating object is equal to one-half the objects rotational inertia [I] times the angular velocity [ω] of the object squared. Kinetic energy is measured in joules, the rotational inertia is measured in kilograms times meters squared, and angular velocity in radians per second.

KE_linear = (1/2) × mv²

linear energy: the kinetic energy [ke] of a moving object is equal to one-half the mass [m] of the object times the velocity [v] of the object squared. Kinetic energy is measured in joules, the mass in kilograms, and velocity in meters per second.

KE_Total = KE_Linear + KE_Rotational

kinetic energy: the kinetic energy total [ke] of an object is equal to the objects linear kinetic energy plus the sum of all the rotational kinetic energy. All energy is measured in joules.

*Can't find what you're looking for? Ask Doc Fizzix »